Trigonometric Functions

Trigonometric Functions

Trig Functions: The Functions 
  

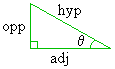
sine(q) = opp/hyp	cosecant(q) = hyp/opp
cosine(q) = adj/hyp	secant(q) = hyp/adj
tangent(q) = opp/adj	cotangent(q) = adj/opp

The functions are usually abbreviated: sine (sin), cosine (cos), tangent (tan) cosecant (csc), secant (sec), and cotangent (cot). 
It is often simpler to memorize the the trig functions in terms of only sine and cosine: 

sine(q) = opp/hyp	csc(q) = 1/sin(q)
cos(q) = adj/hyp	sec(q) = 1/COs(q)
tan(q) = sin(q)/cos(q)	cot(q) = 1/tan(q)

Inverse Functions

arcsine(opp/hyp) = q	arccosecant(hyp/opp) = q
arccosine(adj/hyp) = q	arcsecant(hyp/adj) = q
arctangent(opp/adj) = q	arccotangent(adj/opp) = q

The functions are usually abbreviated: 
arcsine (arcsin)
arccosine (arccos)
arctangent (arctan)
arccosecant (arccsc)
arcsecant (arcsec)
arccotangent (arccot). 
According to the standard notation for inverse functions (f^-1), you will also often see these written as sin^-1, cos-1, tan^-1 arccsc^-1, arcsec^-1, and arccot^-1. Beware, though, there is another common notation that writes the square of the trig functions, such as (sin(x))² as sin²(x). This can be confusing, for you then might then be lead to think that sin^-1(x) = (sin(x))^-1, which is not true. The negative one superscript here is a special notation that denotes inverse functions (not multiplicative inverses).