Projectile motion
is a form of
motion
where a particle (called a
projectile
) is thrown obliquely near the earth's surface, and
it moves along a curved path under the action of
gravity
. The path followed by a projectile motion is called its
trajectory
. Projectile motion only occurs when there is one force applied at the beginning of the trajectory after which there is no interference apart from gravity.
 , that is,
, that is,

The initial velocity
If the projectile is launched with an initial velocity v 0 , then it can be written as .
.
 ,
,
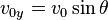 .
.
 .
.
Kinematic quantities of projectile motion
In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other.Acceleration
Since there is no acceleration in the horizontal direction velocity in horizontal direction is constant which is equal to ucosα. The vertical motion of the projectile is the motion of a particle during its free fall. Here the acceleration is constant, equal to g . The components of the acceleration: ,
,
 .
.
Velocity
The horizontal component of the velocity remains unchanged throughout the motion. The vertical component of the velocity increases linearly, because the acceleration is constant. At any time t , the components of the velocity: ,
,
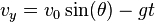 .
.
 .
.
Displacement
At any time t , the projectile's horizontal and vertical displacement :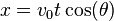 ,
,
 .
.
Parabolic trajectory
Main article:
Trajectory of a projectile
Consider the equations,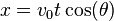 ,
,
 .
.
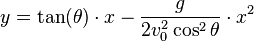 ,
,
 ,
,
The maximum height of projectile
The highest height which the object will reach is known as the peak of the object's motion. The increase of the height will last, until , that is,
, that is,
 .
.
 .
.

 .
.
Additional equation
For the relation between the range (R) on the horizontal plane, the maximum height (h) reached at t/2 and angle of launch, the equation below has been developed.
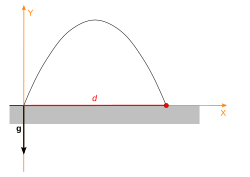
The maximum distance of projectile
Main article:
Range of a projectile
The horizontal range
d
of the projectile is the horizontal distance the projectile has travelled when it returns to its initial height (
y
= 0).
 .
.
 ,
,
 ,
,
 .
.
Application of the work energy theorem
According to the work-energy theorem the vertical component of velocity: .
.
References
- Budó Ágoston: Kísérleti fizika I. ,Budapest, Tankönyvkiadó, 1986. ISBN 963 17 8772 9 (Hungarian)
- Ifj. Zátonyi Sándor: Fizika 9. ,Budapest, Nemzeti Tankönyvkiadó, 2009. ISBN 978-963-19-6082-2 (Hungarian)
- Hack Frigyes: Négyjegyű függvénytáblázatok, összefüggések és adatok , Budapest, Nemzeti Tankönyvkiadó, 2004. ISBN 963-19-3506-X (Hungarian)
Notes
- ^ The g is the acceleration due to gravity. (9.81 m/s 2 near the surface of the Earth).
- Since the value of g is not specific the body with high velocity over g limit cannot be measured using the concept of the projectile motion

 .
.
 ,
,
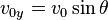 .
.
 .
.
 ,
,
 .
.
 ,
,
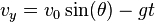 .
.
 .
.

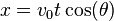 ,
,
 .
.
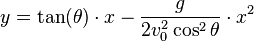 ,
,
 ,
,

 .
.
 .
.

 .
.
 .
.
 ,
,
 ,
,
 .
.
 .
.
No comments:
Post a Comment