Introduction to Sets
Forget everything you know about numbers.
In fact, forget you even know what a number is.
This is where mathematics starts.
Instead of math with numbers, we will now think about math with "things".
Definition
What is a set? Well, simply put, it's a collection.
First you specify a common property among "things" (this word will be defined later) and then you gather up all the "things" that have this common property.
For example, the items you wear: these would include shoes, socks, hat, shirt, pants, and so on.
I'm sure you could come up with at least a hundred.
This is known as a set.
In mathematics, a set is a collection of distinct objects, considered as an object in its own right. For example, the numbers 2, 4, and 6 are distinct objects when considered separately, but when they are considered collectively they form a single set of size three, written {2,4,6}. Sets are one of the most fundamental concepts in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from which nearly all of mathematics can be derived. In mathematics education, elementary topics such as Venn diagrams are taught at a young age, while more advanced concepts are taught as part of a university degree. The term itself was coined by Bolzano in his work The Paradoxes of the Infinite.
Describing sets
There are two ways of describing, or specifying the members of, a set. One way is by intensional definition, using a rule or semantic description:
A is the set whose members are the first four positive integers.
B is the set of colors of the French flag.
The second way is by extension – that is, listing each member of the set. An extensional definition is denoted by enclosing the list of members in curly brackets:
C = {4, 2, 1, 3}
D = {blue, white, red}.
Every element of a set must be unique; no two members may be identical. (A multiset is a generalized concept of a set that relaxes this criterion.) All set operations preserve this property. The order in which the elements of a set or multiset are listed is irrelevant (unlike for a sequence or tuple). Combining these two ideas into an example
{6, 11} = {11, 6} = {11, 6, 6, 11}
because the extensional specification means merely that each of the elements listed is a member of the set.
For sets with many elements, the enumeration of members can be abbreviated. For instance, the set of the first thousand positive integers may be specified extensionally as:
{1, 2, 3, ..., 1000},
where the ellipsis ("...") indicates that the list continues in the obvious way. Ellipses may also be used where sets have infinitely many members. Thus the set of positive even numbers can be written as {2, 4, 6, 8, ... }.
The notation with braces may also be used in an intensional specification of a set. In this usage, the braces have the meaning "the set of all ...". So, E = {playing card suits} is the set whose four members are ♠, ♦, ♥, and ♣. A more general form of this is set-builder notation, through which, for instance, the set F of the twenty smallest integers that are four less than perfect squares can be denoted:
F = {n2 − 4 : n is an integer; and 0 ≤ n ≤ 19}.
In this notation, the colon (":") means "such that", and the description can be interpreted as "F is the set of all numbers of the form n2 − 4, such that n is a whole number in the range from 0 to 19 inclusive." Sometimes the vertical bar ("|") is used instead of the colon.
One often has the choice of specifying a set intensionally or extensionally. In the examples above, for instance, A = C and B = D.
Subsets
If every member of set A is also a member of set B, then A is said to be a subset of B, written A ⊆ B (also pronounced A is contained in B). Equivalently, we can write B ⊇ A, read as B is a superset of A, B includes A, or B contains A. The relationship between sets established by ⊆ is called inclusion or containment.
If A is a subset of, but not equal to, B, then A is called a proper subset of B, written A ⊊ B (A is a proper subset of B) or B ⊋ A (B is a proper superset of A).
Note that the expressions A ⊂ B and B ⊃ A are used differently by different authors; some authors use them to mean the same as A ⊆ B (respectively B ⊇ A), whereas other use them to mean the same as A ⊊ B (respectively B ⊋ A).
Example:
The set of all men is a proper subset of the set of all people.
{1, 3} ⊊ {1, 2, 3, 4}.
{1, 2, 3, 4} ⊆ {1, 2, 3, 4}.
The empty set is a subset of every set and every set is a subset of itself:
∅ ⊆ A.
A ⊆ A.
An obvious but useful identity, which can often be used to show that two seemingly different sets are equal:
A = B if and only if A ⊆ B and B ⊆ A.
A partition of a set S is a set of nonempty subsets of S such that every element x in S is in exactly one of these subsets.
Power sets
The power set of a set S is the set of all subsets of S, including S itself and the empty set. For example, the power set of the set {1, 2, 3} is {{1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, ∅}. The power set of a set S usually written as P(S).
The power set of a finite set with n elements has 2n elements. This relationship is one of the reasons for the terminology power set. For example, the set {1, 2, 3} contains three elements, and the power set shown above contains 23 = 8 elements.
The power set of an infinite (either countable or uncountable) set is always uncountable. Moreover, the power set of a set is always strictly "bigger" than the original set in the sense that there is no way to pair the elements of a set S with the elements of its power set P(S) such that every element of S set is paired with exactly one element of P(S), and every element of P(S) is paired with exactly one element of S. (There is never a bijection from S onto P(S).)
Every partition of a set S is a subset of the powerset of S.
Cardinality
The cardinality | S | of a set S is "the number of members of S." For example, if B = {blue, white, red}, | B | = 3.
There is a unique set with no members and zero cardinality, which is called the empty set (or the null set) and is denoted by the symbol ∅ (other notations are used; see empty set). For example, the set of all three-sided squares has zero members and thus is the empty set. Though it may seem trivial, the empty set, like the number zero, is important in mathematics; indeed, the existence of this set is one of the fundamental concepts of axiomatic set theory.
Some sets have infinite cardinality. The set N of natural numbers, for instance, is infinite. Some infinite cardinalities are greater than others. For instance, the set of real numbers has greater cardinality than the set of natural numbers. However, it can be shown that the cardinality of (which is to say, the number of points on) a straight line is the same as the cardinality of any segment of that line, of the entire plane, and indeed of any finite-dimensional Euclidean space.
Special sets
There are some sets that hold great mathematical importance and are referred to with such regularity that they have acquired special names and notational conventions to identify them. One of these is the empty set, denoted {} or ∅. Another is the unit set {x}, which contains exactly one element, namely x.[2] Many of these sets are represented using blackboard bold or bold typeface. Special sets of numbers include:
P or ℙ, denoting the set of all primes: P = {2, 3, 5, 7, 11, 13, 17, ...}.
N or ℕ, denoting the set of all natural numbers: N = {1, 2, 3, . . .} (sometimes defined containing 0).
Z or ℤ, denoting the set of all integers (whether positive, negative or zero): Z = {..., −2, −1, 0, 1, 2, ...}.
Q or ℚ, denoting the set of all rational numbers (that is, the set of all proper and improper fractions): Q = {a/b : a, b ∈ Z, b ≠ 0}. For example, 1/4 ∈ Q and 11/6 ∈ Q. All integers are in this set since every integer a can be expressed as the fraction a/1 (Z ⊊ Q).
R or ℝ, denoting the set of all real numbers. This set includes all rational numbers, together with all irrational numbers (that is, numbers that cannot be rewritten as fractions, such as √2, as well as transcendental numbers such as π, e and numbers that cannot be defined).
C or ℂ, denoting the set of all complex numbers: C = {a + bi : a, b ∈ R}. For example, 1 + 2i ∈ C.
H or ℍ, denoting the set of all quaternions: H = {a + bi + cj + dk : a, b, c, d ∈ R}. For example, 1 + i + 2j − k ∈ H.
Positive and negative sets are denoted by a superscript - or +, for example: ℚ+ represents the set of positive rational numbers.
Each of the above sets of numbers has an infinite number of elements, and each can be considered to be a proper subset of the sets listed below it. The primes are used less frequently than the others outside of number theory and related fields.
Basic operations
There are several fundamental operations for constructing new sets from given sets.
Unions
Two sets can be "added" together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either A or B.
Examples:
{1, 2} ∪ {red, white} ={1, 2, red, white}.
{1, 2, green} ∪ {red, white, green} ={1, 2, red, white, green}.
{1, 2} ∪ {1, 2} = {1, 2}.
Some basic properties of unions:
A ∪ B = B ∪ A.
A ∪ (B ∪ C) = (A ∪ B) ∪ C.
A ⊆ (A ∪ B).
A ∪ A = A.
A ∪ ∅ = A.
A ⊆ B if and only if A ∪ B = B.
Intersections
A new set can also be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.
Examples:
{1, 2} ∩ {red, white} = ∅.
{1, 2, green} ∩ {red, white, green} = {green}.
{1, 2} ∩ {1, 2} = {1, 2}.
Some basic properties of intersections:
A ∩ B = B ∩ A.
A ∩ (B ∩ C) = (A ∩ B) ∩ C.
A ∩ B ⊆ A.
A ∩ A = A.
A ∩ ∅ = ∅.
A ⊆ B if and only if A ∩ B = A.
Complements
Two sets can also be "subtracted". The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A \ B (or A − B), is the set of all elements that are members of A but not members of B. Note that it is valid to "subtract" members of a set that are not in the set, such as removing the element green from the set {1, 2, 3}; doing so has no effect.
In certain settings all sets under discussion are considered to be subsets of a given universal set U. In such cases, U \ A is called the absolute complement or simply complement of A, and is denoted by A′.
Examples:
{1, 2} \ {red, white} = {1, 2}.
{1, 2, green} \ {red, white, green} = {1, 2}.
{1, 2} \ {1, 2} = ∅.
{1, 2, 3, 4} \ {1, 3} = {2, 4}.
If U is the set of integers, E is the set of even integers, and O is the set of odd integers, then U \ E = E′ = O.
An extension of the complement is the symmetric difference, defined for sets A, B as
For example, the symmetric difference of {7,8,9,10} and {9,10,11,12} is the set {7,8,11,12}.
Cartesian product
A new set can be constructed by associating every element of one set with every element of another set. The Cartesian product of two sets A and B, denoted by A × B is the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.
Examples:
{1, 2} × {red, white} = {(1, red), (1, white), (2, red), (2, white)}.
{1, 2, green} × {red, white, green} = {(1, red), (1, white), (1, green), (2, red), (2, white), (2, green), (green, red), (green, white), (green, green)}.
{1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
Some basic properties of cartesian products:
A × ∅ = ∅.
A × (B ∪ C) = (A × B) ∪ (A × C).
(A ∪ B) × C = (A × C) ∪ (B × C).
Let A and B be finite sets. Then
| A × B | = | B × A | = | A | × | B |.
Applications
Set theory is seen as the foundation from which virtually all of mathematics can be derived. For example, structures in abstract algebra, such as groups, fields and rings, are sets closed under one or more operations.
One of the main applications of naive set theory is constructing relations. A relation from a domain A to a codomain B is a subset of the Cartesian product A × B. Given this concept, we are quick to see that the set F of all ordered pairs (x, x2), where x is real, is quite familiar. It has a domain set R and a codomain set that is also R, because the set of all squares is subset of the set of all reals. If placed in functional notation, this relation becomes f(x) = x2. The reason these two are equivalent is for any given value, y that the function is defined for, its corresponding ordered pair, (y, y2) is a member of the set F.
Axiomatic set theory
Although initially naive set theory, which defines a set merely as any well-defined collection, was well accepted, it soon ran into several obstacles. It was found that this definition spawned several paradoxes, most notably:
Russell's paradox—It shows that the "set of all sets that do not contain themselves," i.e. the "set" { x : x is a set and x ∉ x } does not exist.
Cantor's paradox—It shows that "the set of all sets" cannot exist.
The reason is that the phrase well-defined is not very well defined. It was important to free set theory of these paradoxes because nearly all of mathematics was being redefined in terms of set theory. In an attempt to avoid these paradoxes, set theory was axiomatized based on first-order logic, and thus axiomatic set theory was born.
For most purposes however, naive set theory is still useful.
Principle of inclusion and exclusion
This principle gives us the cardinality of the union of sets. |A1 ∪ A2 ∪ A3 ∪ A4 ∪ ... ∪ An|=(|A1| + |A2| + |A3| +...+ |An|)-(|A1 ∩ A2| +|A1 ∩ A3| + ....+|An-1 ∩ An|) + .........+(−1)^{n-1}(|A1 ∩ A2 ∩ A3 ∩.....∩ An|)
Forget everything you know about numbers.
In fact, forget you even know what a number is.
This is where mathematics starts.
Instead of math with numbers, we will now think about math with "things".
Definition
What is a set? Well, simply put, it's a collection.
First you specify a common property among "things" (this word will be defined later) and then you gather up all the "things" that have this common property.
For example, the items you wear: these would include shoes, socks, hat, shirt, pants, and so on.
I'm sure you could come up with at least a hundred.
This is known as a set.
In mathematics, a set is a collection of distinct objects, considered as an object in its own right. For example, the numbers 2, 4, and 6 are distinct objects when considered separately, but when they are considered collectively they form a single set of size three, written {2,4,6}. Sets are one of the most fundamental concepts in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from which nearly all of mathematics can be derived. In mathematics education, elementary topics such as Venn diagrams are taught at a young age, while more advanced concepts are taught as part of a university degree. The term itself was coined by Bolzano in his work The Paradoxes of the Infinite.
Describing sets
There are two ways of describing, or specifying the members of, a set. One way is by intensional definition, using a rule or semantic description:
A is the set whose members are the first four positive integers.
B is the set of colors of the French flag.
The second way is by extension – that is, listing each member of the set. An extensional definition is denoted by enclosing the list of members in curly brackets:
C = {4, 2, 1, 3}
D = {blue, white, red}.
Every element of a set must be unique; no two members may be identical. (A multiset is a generalized concept of a set that relaxes this criterion.) All set operations preserve this property. The order in which the elements of a set or multiset are listed is irrelevant (unlike for a sequence or tuple). Combining these two ideas into an example
{6, 11} = {11, 6} = {11, 6, 6, 11}
because the extensional specification means merely that each of the elements listed is a member of the set.
For sets with many elements, the enumeration of members can be abbreviated. For instance, the set of the first thousand positive integers may be specified extensionally as:
{1, 2, 3, ..., 1000},
where the ellipsis ("...") indicates that the list continues in the obvious way. Ellipses may also be used where sets have infinitely many members. Thus the set of positive even numbers can be written as {2, 4, 6, 8, ... }.
The notation with braces may also be used in an intensional specification of a set. In this usage, the braces have the meaning "the set of all ...". So, E = {playing card suits} is the set whose four members are ♠, ♦, ♥, and ♣. A more general form of this is set-builder notation, through which, for instance, the set F of the twenty smallest integers that are four less than perfect squares can be denoted:
F = {n2 − 4 : n is an integer; and 0 ≤ n ≤ 19}.
In this notation, the colon (":") means "such that", and the description can be interpreted as "F is the set of all numbers of the form n2 − 4, such that n is a whole number in the range from 0 to 19 inclusive." Sometimes the vertical bar ("|") is used instead of the colon.
One often has the choice of specifying a set intensionally or extensionally. In the examples above, for instance, A = C and B = D.
Subsets
If every member of set A is also a member of set B, then A is said to be a subset of B, written A ⊆ B (also pronounced A is contained in B). Equivalently, we can write B ⊇ A, read as B is a superset of A, B includes A, or B contains A. The relationship between sets established by ⊆ is called inclusion or containment.
If A is a subset of, but not equal to, B, then A is called a proper subset of B, written A ⊊ B (A is a proper subset of B) or B ⊋ A (B is a proper superset of A).
Note that the expressions A ⊂ B and B ⊃ A are used differently by different authors; some authors use them to mean the same as A ⊆ B (respectively B ⊇ A), whereas other use them to mean the same as A ⊊ B (respectively B ⊋ A).
Example:
The set of all men is a proper subset of the set of all people.
{1, 3} ⊊ {1, 2, 3, 4}.
{1, 2, 3, 4} ⊆ {1, 2, 3, 4}.
The empty set is a subset of every set and every set is a subset of itself:
∅ ⊆ A.
A ⊆ A.
An obvious but useful identity, which can often be used to show that two seemingly different sets are equal:
A = B if and only if A ⊆ B and B ⊆ A.
A partition of a set S is a set of nonempty subsets of S such that every element x in S is in exactly one of these subsets.
 |
| A is Subset of B |
Power sets
The power set of a set S is the set of all subsets of S, including S itself and the empty set. For example, the power set of the set {1, 2, 3} is {{1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, ∅}. The power set of a set S usually written as P(S).
The power set of a finite set with n elements has 2n elements. This relationship is one of the reasons for the terminology power set. For example, the set {1, 2, 3} contains three elements, and the power set shown above contains 23 = 8 elements.
The power set of an infinite (either countable or uncountable) set is always uncountable. Moreover, the power set of a set is always strictly "bigger" than the original set in the sense that there is no way to pair the elements of a set S with the elements of its power set P(S) such that every element of S set is paired with exactly one element of P(S), and every element of P(S) is paired with exactly one element of S. (There is never a bijection from S onto P(S).)
Every partition of a set S is a subset of the powerset of S.
Cardinality
The cardinality | S | of a set S is "the number of members of S." For example, if B = {blue, white, red}, | B | = 3.
There is a unique set with no members and zero cardinality, which is called the empty set (or the null set) and is denoted by the symbol ∅ (other notations are used; see empty set). For example, the set of all three-sided squares has zero members and thus is the empty set. Though it may seem trivial, the empty set, like the number zero, is important in mathematics; indeed, the existence of this set is one of the fundamental concepts of axiomatic set theory.
Some sets have infinite cardinality. The set N of natural numbers, for instance, is infinite. Some infinite cardinalities are greater than others. For instance, the set of real numbers has greater cardinality than the set of natural numbers. However, it can be shown that the cardinality of (which is to say, the number of points on) a straight line is the same as the cardinality of any segment of that line, of the entire plane, and indeed of any finite-dimensional Euclidean space.
Special sets
There are some sets that hold great mathematical importance and are referred to with such regularity that they have acquired special names and notational conventions to identify them. One of these is the empty set, denoted {} or ∅. Another is the unit set {x}, which contains exactly one element, namely x.[2] Many of these sets are represented using blackboard bold or bold typeface. Special sets of numbers include:
P or ℙ, denoting the set of all primes: P = {2, 3, 5, 7, 11, 13, 17, ...}.
N or ℕ, denoting the set of all natural numbers: N = {1, 2, 3, . . .} (sometimes defined containing 0).
Z or ℤ, denoting the set of all integers (whether positive, negative or zero): Z = {..., −2, −1, 0, 1, 2, ...}.
Q or ℚ, denoting the set of all rational numbers (that is, the set of all proper and improper fractions): Q = {a/b : a, b ∈ Z, b ≠ 0}. For example, 1/4 ∈ Q and 11/6 ∈ Q. All integers are in this set since every integer a can be expressed as the fraction a/1 (Z ⊊ Q).
R or ℝ, denoting the set of all real numbers. This set includes all rational numbers, together with all irrational numbers (that is, numbers that cannot be rewritten as fractions, such as √2, as well as transcendental numbers such as π, e and numbers that cannot be defined).
C or ℂ, denoting the set of all complex numbers: C = {a + bi : a, b ∈ R}. For example, 1 + 2i ∈ C.
H or ℍ, denoting the set of all quaternions: H = {a + bi + cj + dk : a, b, c, d ∈ R}. For example, 1 + i + 2j − k ∈ H.
Positive and negative sets are denoted by a superscript - or +, for example: ℚ+ represents the set of positive rational numbers.
Each of the above sets of numbers has an infinite number of elements, and each can be considered to be a proper subset of the sets listed below it. The primes are used less frequently than the others outside of number theory and related fields.
Basic operations
There are several fundamental operations for constructing new sets from given sets.
Unions
Two sets can be "added" together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either A or B.
Examples:
{1, 2} ∪ {red, white} ={1, 2, red, white}.
{1, 2, green} ∪ {red, white, green} ={1, 2, red, white, green}.
{1, 2} ∪ {1, 2} = {1, 2}.
Some basic properties of unions:
A ∪ B = B ∪ A.
A ∪ (B ∪ C) = (A ∪ B) ∪ C.
A ⊆ (A ∪ B).
A ∪ A = A.
A ∪ ∅ = A.
A ⊆ B if and only if A ∪ B = B.
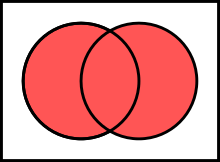 |
| The union of A and B, denoted A ∪ B |
Intersections
A new set can also be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.
Examples:
{1, 2} ∩ {red, white} = ∅.
{1, 2, green} ∩ {red, white, green} = {green}.
{1, 2} ∩ {1, 2} = {1, 2}.
Some basic properties of intersections:
A ∩ B = B ∩ A.
A ∩ (B ∩ C) = (A ∩ B) ∩ C.
A ∩ B ⊆ A.
A ∩ A = A.
A ∩ ∅ = ∅.
A ⊆ B if and only if A ∩ B = A.
 |
| The intersection of A and B, denoted A ∩ B. |
Complements
Two sets can also be "subtracted". The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A \ B (or A − B), is the set of all elements that are members of A but not members of B. Note that it is valid to "subtract" members of a set that are not in the set, such as removing the element green from the set {1, 2, 3}; doing so has no effect.
In certain settings all sets under discussion are considered to be subsets of a given universal set U. In such cases, U \ A is called the absolute complement or simply complement of A, and is denoted by A′.
Examples:
{1, 2} \ {red, white} = {1, 2}.
{1, 2, green} \ {red, white, green} = {1, 2}.
{1, 2} \ {1, 2} = ∅.
{1, 2, 3, 4} \ {1, 3} = {2, 4}.
If U is the set of integers, E is the set of even integers, and O is the set of odd integers, then U \ E = E′ = O.
An extension of the complement is the symmetric difference, defined for sets A, B as
For example, the symmetric difference of {7,8,9,10} and {9,10,11,12} is the set {7,8,11,12}.
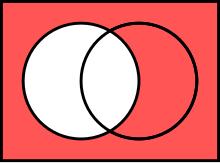 |
| The complement of A in U |
Cartesian product
A new set can be constructed by associating every element of one set with every element of another set. The Cartesian product of two sets A and B, denoted by A × B is the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.
Examples:
{1, 2} × {red, white} = {(1, red), (1, white), (2, red), (2, white)}.
{1, 2, green} × {red, white, green} = {(1, red), (1, white), (1, green), (2, red), (2, white), (2, green), (green, red), (green, white), (green, green)}.
{1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
Some basic properties of cartesian products:
A × ∅ = ∅.
A × (B ∪ C) = (A × B) ∪ (A × C).
(A ∪ B) × C = (A × C) ∪ (B × C).
Let A and B be finite sets. Then
| A × B | = | B × A | = | A | × | B |.
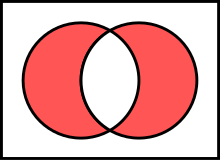 |
| The symmetric difference of A and B |
Applications
Set theory is seen as the foundation from which virtually all of mathematics can be derived. For example, structures in abstract algebra, such as groups, fields and rings, are sets closed under one or more operations.
One of the main applications of naive set theory is constructing relations. A relation from a domain A to a codomain B is a subset of the Cartesian product A × B. Given this concept, we are quick to see that the set F of all ordered pairs (x, x2), where x is real, is quite familiar. It has a domain set R and a codomain set that is also R, because the set of all squares is subset of the set of all reals. If placed in functional notation, this relation becomes f(x) = x2. The reason these two are equivalent is for any given value, y that the function is defined for, its corresponding ordered pair, (y, y2) is a member of the set F.
Axiomatic set theory
Although initially naive set theory, which defines a set merely as any well-defined collection, was well accepted, it soon ran into several obstacles. It was found that this definition spawned several paradoxes, most notably:
Russell's paradox—It shows that the "set of all sets that do not contain themselves," i.e. the "set" { x : x is a set and x ∉ x } does not exist.
Cantor's paradox—It shows that "the set of all sets" cannot exist.
The reason is that the phrase well-defined is not very well defined. It was important to free set theory of these paradoxes because nearly all of mathematics was being redefined in terms of set theory. In an attempt to avoid these paradoxes, set theory was axiomatized based on first-order logic, and thus axiomatic set theory was born.
For most purposes however, naive set theory is still useful.
Principle of inclusion and exclusion
This principle gives us the cardinality of the union of sets. |A1 ∪ A2 ∪ A3 ∪ A4 ∪ ... ∪ An|=(|A1| + |A2| + |A3| +...+ |An|)-(|A1 ∩ A2| +|A1 ∩ A3| + ....+|An-1 ∩ An|) + .........+(−1)^{n-1}(|A1 ∩ A2 ∩ A3 ∩.....∩ An|)

No comments:
Post a Comment