Momentum
In classical mechanics, linear momentum or translational momentum (pl. momenta; SI unit kg m/s, or equivalently, N s) is the product of the mass and velocity of an object. For example, a heavy truck moving fast has a large momentum—it takes a large and prolonged force to get the truck up to this speed, and it takes a large and prolonged force to bring it to a stop afterwards. If the truck were lighter, or moving more slowly, then it would have less momentum.
Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude:
Linear momentum is also a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum cannot change. In classical mechanics, conservation of linear momentum is implied by Newton's laws; but it also holds in special relativity (with a modified formula) and, with appropriate definitions, a (generalized) linear momentum conservation law holds in electrodynamics, quantum mechanics, quantum field theory, and general relativity.
Newtonian mechanics
Momentum has a direction as well as magnitude. Quantities that have both a magnitude and a direction are known as vector quantities. Because momentum has a direction, it can be used to predict the resulting direction of objects after they collide, as well as their speeds. Below, the basic properties of momentum are described in one dimension. The vector equations are almost identical to the scalar equations (see multiple dimensions).
Single particle
The momentum of a particle is traditionally represented by the letter p. It is the product of two quantities, the mass (represented by the letter m) and velocity (v):
A
Newton's cradle
demonstrates conservation of momentum.
Elastic collision of equal masses
Elastic collision of unequal masses
In classical mechanics, linear momentum or translational momentum (pl. momenta; SI unit kg m/s, or equivalently, N s) is the product of the mass and velocity of an object. For example, a heavy truck moving fast has a large momentum—it takes a large and prolonged force to get the truck up to this speed, and it takes a large and prolonged force to bring it to a stop afterwards. If the truck were lighter, or moving more slowly, then it would have less momentum.
Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude:
Newtonian mechanics
Momentum has a direction as well as magnitude. Quantities that have both a magnitude and a direction are known as vector quantities. Because momentum has a direction, it can be used to predict the resulting direction of objects after they collide, as well as their speeds. Below, the basic properties of momentum are described in one dimension. The vector equations are almost identical to the scalar equations (see multiple dimensions).
Single particle
The momentum of a particle is traditionally represented by the letter p. It is the product of two quantities, the mass (represented by the letter m) and velocity (v):
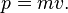
No comments:
Post a Comment