Force
In physics, a force is any influence that causes an object to undergo a certain change, either concerning its movement, direction, or geometrical construction. In other words, a force can cause an object with mass to change its velocity (which includes to begin moving from a state of rest), i.e., to accelerate, or a flexible object to deform, or both. Force can also be described by intuitive concepts such as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newtons and represented by the symbol F.
The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. As a formula, this is expressed as:
where the arrows imply a vector quantity possessing both magnitude and direction.
Related concepts to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque which produces changes in rotational speed of an object. In an extended body, each part usually applies forces on the adjacent parts; the distribution of such forces through the body is the so-called mechanical stress. Pressure is a simple type of stress. Stress usually causes deformation of solid materials, or flow in fluids.
Development of the Concept
Philosophers in antiquity used the concept of force in the study of stationary and moving objects and simple machines, but thinkers such as Aristotle and Archimedes retained fundamental errors in understanding force. In part this was due to an incomplete understanding of the sometimes non-obvious force of friction, and a consequently inadequate view of the nature of natural motion. A fundamental error was the belief that a force is required to maintain motion, even at a constant velocity. Most of the previous misunderstandings about motion and force were eventually corrected by Sir Isaac Newton; with his mathematical insight, he formulated laws of motion that were not improved-on for nearly three hundred years. By the early 20th century, Einstein developed a theory of relativity that correctly predicted the action of forces on objects with increasing momenta near the speed of light, and also provided insight into the forces produced by gravitation and inertia.
With modern insights into quantum mechanics and technology that can accelerate particles close to the speed of light, particle physics has devised a Standard Model to describe forces between particles smaller than atoms. The Standard Model predicts that exchanged particles called gauge bosons are the fundamental means by which forces are emitted and absorbed. Only four main interactions are known: in order of decreasing strength, they are: strong, electromagnetic, weak, and gravitational. High-energy particle physics observations made during the 1970s and 1980s confirmed that the weak and electromagnetic forces are expressions of a more fundamental electroweak interaction.
Pre-Newtonian Concepts
Since antiquity the concept of force has been recognized as integral to the functioning of each of the simple machines. The mechanical advantage given by a simple machine allowed for less force to be used in exchange for that force acting over a greater distance for the same amount of work. Analysis of the characteristics of forces ultimately culminated in the work of Archimedes who was especially famous for formulating a treatment of buoyant forces inherent in fluids.
Aristotle provided a philosophical discussion of the concept of a force as an integral part of Aristotelian cosmology. In Aristotle's view, the natural world held four elements that existed in "natural states". Aristotle believed that it was the natural state of objects with mass on Earth, such as the elements water and earth, to be motionless on the ground and that they tended towards that state if left alone. He distinguished between the innate tendency of objects to find their "natural place" (e.g., for heavy bodies to fall), which led to "natural motion", and unnatural or forced motion, which required continued application of a force. This theory, based on the everyday experience of how objects move, such as the constant application of a force needed to keep a cart moving, had conceptual trouble accounting for the behavior of projectiles, such as the flight of arrows. The place where forces were applied to projectiles was only at the start of the flight, and while the projectile sailed through the air, no discernible force acts on it. Aristotle was aware of this problem and proposed that the air displaced through the projectile's path provided the needed force to continue the projectile moving. This explanation demands that air is needed for projectiles and that, for example, in a vacuum, no projectile would move after the initial push. Additional problems with the explanation include the fact that air resists the motion of the projectiles.
Aristotelian physics began facing criticism in Medieval science, first by John Philoponus in the 6th century.
The shortcomings of Aristotelian physics would not be fully corrected until the 17th century work of Galileo Galilei, who was influenced by the late Medieval idea that objects in forced motion carried an innate force of impetus. Galileo constructed an experiment in which stones and cannonballs were both rolled down an incline to disprove the Aristotelian theory of motion early in the 17th century. He showed that the bodies were accelerated by gravity to an extent which was independent of their mass and argued that objects retain their velocity unless acted on by a force, for example friction.
Newtonian Mechanics
Sir Isaac Newton sought to describe the motion of all objects using the concepts of inertia and force, and in doing so he found that they obey certain conservation laws. In 1687, Newton went on to publish his thesis Philosophiae Naturalis Principia Mathematica. In this work Newton set out three laws of motion that to this day are the way forces are described in physics.
Descriptions
Since forces are perceived as pushes or pulls, this can provide an intuitive understanding for describing forces. As with other physical concepts (e.g. temperature), the intuitive understanding of forces is quantified using precise operational definitions that are consistent with direct observations and compared to a standard measurement scale. Through experimentation, it is determined that laboratory measurements of forces are fully consistent with the conceptual definition of force offered by Newtonian mechanics.
Forces act in a particular direction and have sizes dependent upon how strong the push or pull is. Because of these characteristics, forces are classified as "vector quantities". This means that forces follow a different set of mathematical rules than physical quantities that do not have direction (denoted scalar quantities). For example, when determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result. If both of these pieces of information are not known for each force, the situation is ambiguous. For example, if you know that two people are pulling on the same rope with known magnitudes of force but you do not know which direction either person is pulling, it is impossible to determine what the acceleration of the rope will be. The two people could be pulling against each other as in tug of war or the two people could be pulling in the same direction. In this simple one-dimensional example, without knowing the direction of the forces it is impossible to decide whether the net force is the result of adding the two force magnitudes or subtracting one from the other. Associating forces with vectors avoids such problems.
Historically, forces were first quantitatively investigated in conditions of static equilibrium where several forces canceled each other out. Such experiments demonstrate the crucial properties that forces are additive vector quantities: they have magnitude and direction.When two forces act on a point particle, the resulting force, the resultant (also called the net force), can be determined by following the parallelogram rule of vector addition: the addition of two vectors represented by sides of a parallelogram, gives an equivalent resultant vector which is equal in magnitude and direction to the transversal of the parallelogram.The magnitude of the resultant varies from the difference of the magnitudes of the two forces to their sum, depending on the angle between their lines of action. However, if the forces are acting on an extended body, their respective lines of application must also be specified in order to account for their effects on the motion of the body.
Free-body diagrams can be used as a convenient way to keep track of forces acting on a system. Ideally, these diagrams are drawn with the angles and relative magnitudes of the force vectors preserved so that graphical vector addition can be done to determine the net force.
As well as being added, forces can also be resolved into independent components at right angles to each other. A horizontal force pointing northeast can therefore be split into two forces, one pointing north, and one pointing east. Summing these component forces using vector addition yields the original force. Resolving force vectors into components of a set of basis vectors is often a more mathematically clean way to describe forces than using magnitudes and directions.This is because, for orthogonal components, the components of the vector sum are uniquely determined by the scalar addition of the components of the individual vectors. Orthogonal components are independent of each other because forces acting at ninety degrees to each other have no effect on the magnitude or direction of the other. Choosing a set of orthogonal basis vectors is often done by considering what set of basis vectors will make the mathematics most convenient. Choosing a basis vector that is in the same direction as one of the forces is desirable, since that force would then have only one non-zero component. Orthogonal force vectors can be three-dimensional with the third component being at right-angles to the other two.
In physics, a force is any influence that causes an object to undergo a certain change, either concerning its movement, direction, or geometrical construction. In other words, a force can cause an object with mass to change its velocity (which includes to begin moving from a state of rest), i.e., to accelerate, or a flexible object to deform, or both. Force can also be described by intuitive concepts such as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newtons and represented by the symbol F.
The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. As a formula, this is expressed as:
where the arrows imply a vector quantity possessing both magnitude and direction.
Related concepts to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque which produces changes in rotational speed of an object. In an extended body, each part usually applies forces on the adjacent parts; the distribution of such forces through the body is the so-called mechanical stress. Pressure is a simple type of stress. Stress usually causes deformation of solid materials, or flow in fluids.
Development of the Concept
Philosophers in antiquity used the concept of force in the study of stationary and moving objects and simple machines, but thinkers such as Aristotle and Archimedes retained fundamental errors in understanding force. In part this was due to an incomplete understanding of the sometimes non-obvious force of friction, and a consequently inadequate view of the nature of natural motion. A fundamental error was the belief that a force is required to maintain motion, even at a constant velocity. Most of the previous misunderstandings about motion and force were eventually corrected by Sir Isaac Newton; with his mathematical insight, he formulated laws of motion that were not improved-on for nearly three hundred years. By the early 20th century, Einstein developed a theory of relativity that correctly predicted the action of forces on objects with increasing momenta near the speed of light, and also provided insight into the forces produced by gravitation and inertia.
With modern insights into quantum mechanics and technology that can accelerate particles close to the speed of light, particle physics has devised a Standard Model to describe forces between particles smaller than atoms. The Standard Model predicts that exchanged particles called gauge bosons are the fundamental means by which forces are emitted and absorbed. Only four main interactions are known: in order of decreasing strength, they are: strong, electromagnetic, weak, and gravitational. High-energy particle physics observations made during the 1970s and 1980s confirmed that the weak and electromagnetic forces are expressions of a more fundamental electroweak interaction.
Pre-Newtonian Concepts
Since antiquity the concept of force has been recognized as integral to the functioning of each of the simple machines. The mechanical advantage given by a simple machine allowed for less force to be used in exchange for that force acting over a greater distance for the same amount of work. Analysis of the characteristics of forces ultimately culminated in the work of Archimedes who was especially famous for formulating a treatment of buoyant forces inherent in fluids.
Aristotle provided a philosophical discussion of the concept of a force as an integral part of Aristotelian cosmology. In Aristotle's view, the natural world held four elements that existed in "natural states". Aristotle believed that it was the natural state of objects with mass on Earth, such as the elements water and earth, to be motionless on the ground and that they tended towards that state if left alone. He distinguished between the innate tendency of objects to find their "natural place" (e.g., for heavy bodies to fall), which led to "natural motion", and unnatural or forced motion, which required continued application of a force. This theory, based on the everyday experience of how objects move, such as the constant application of a force needed to keep a cart moving, had conceptual trouble accounting for the behavior of projectiles, such as the flight of arrows. The place where forces were applied to projectiles was only at the start of the flight, and while the projectile sailed through the air, no discernible force acts on it. Aristotle was aware of this problem and proposed that the air displaced through the projectile's path provided the needed force to continue the projectile moving. This explanation demands that air is needed for projectiles and that, for example, in a vacuum, no projectile would move after the initial push. Additional problems with the explanation include the fact that air resists the motion of the projectiles.
Aristotelian physics began facing criticism in Medieval science, first by John Philoponus in the 6th century.
The shortcomings of Aristotelian physics would not be fully corrected until the 17th century work of Galileo Galilei, who was influenced by the late Medieval idea that objects in forced motion carried an innate force of impetus. Galileo constructed an experiment in which stones and cannonballs were both rolled down an incline to disprove the Aristotelian theory of motion early in the 17th century. He showed that the bodies were accelerated by gravity to an extent which was independent of their mass and argued that objects retain their velocity unless acted on by a force, for example friction.
 |
| Aristotle famously described a force as anything that causes an object to undergo "unnatural motion" |
Newtonian Mechanics
Sir Isaac Newton sought to describe the motion of all objects using the concepts of inertia and force, and in doing so he found that they obey certain conservation laws. In 1687, Newton went on to publish his thesis Philosophiae Naturalis Principia Mathematica. In this work Newton set out three laws of motion that to this day are the way forces are described in physics.
Descriptions
Since forces are perceived as pushes or pulls, this can provide an intuitive understanding for describing forces. As with other physical concepts (e.g. temperature), the intuitive understanding of forces is quantified using precise operational definitions that are consistent with direct observations and compared to a standard measurement scale. Through experimentation, it is determined that laboratory measurements of forces are fully consistent with the conceptual definition of force offered by Newtonian mechanics.
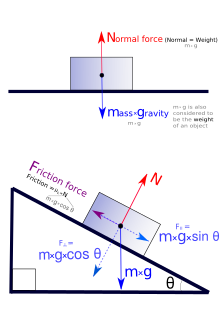 |
| Diagrams of a block on a flat surface and an inclined plane. Forces are resolved and added together to determine their magnitudes and the net force. |
Forces act in a particular direction and have sizes dependent upon how strong the push or pull is. Because of these characteristics, forces are classified as "vector quantities". This means that forces follow a different set of mathematical rules than physical quantities that do not have direction (denoted scalar quantities). For example, when determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result. If both of these pieces of information are not known for each force, the situation is ambiguous. For example, if you know that two people are pulling on the same rope with known magnitudes of force but you do not know which direction either person is pulling, it is impossible to determine what the acceleration of the rope will be. The two people could be pulling against each other as in tug of war or the two people could be pulling in the same direction. In this simple one-dimensional example, without knowing the direction of the forces it is impossible to decide whether the net force is the result of adding the two force magnitudes or subtracting one from the other. Associating forces with vectors avoids such problems.
Historically, forces were first quantitatively investigated in conditions of static equilibrium where several forces canceled each other out. Such experiments demonstrate the crucial properties that forces are additive vector quantities: they have magnitude and direction.When two forces act on a point particle, the resulting force, the resultant (also called the net force), can be determined by following the parallelogram rule of vector addition: the addition of two vectors represented by sides of a parallelogram, gives an equivalent resultant vector which is equal in magnitude and direction to the transversal of the parallelogram.The magnitude of the resultant varies from the difference of the magnitudes of the two forces to their sum, depending on the angle between their lines of action. However, if the forces are acting on an extended body, their respective lines of application must also be specified in order to account for their effects on the motion of the body.
Free-body diagrams can be used as a convenient way to keep track of forces acting on a system. Ideally, these diagrams are drawn with the angles and relative magnitudes of the force vectors preserved so that graphical vector addition can be done to determine the net force.
As well as being added, forces can also be resolved into independent components at right angles to each other. A horizontal force pointing northeast can therefore be split into two forces, one pointing north, and one pointing east. Summing these component forces using vector addition yields the original force. Resolving force vectors into components of a set of basis vectors is often a more mathematically clean way to describe forces than using magnitudes and directions.This is because, for orthogonal components, the components of the vector sum are uniquely determined by the scalar addition of the components of the individual vectors. Orthogonal components are independent of each other because forces acting at ninety degrees to each other have no effect on the magnitude or direction of the other. Choosing a set of orthogonal basis vectors is often done by considering what set of basis vectors will make the mathematics most convenient. Choosing a basis vector that is in the same direction as one of the forces is desirable, since that force would then have only one non-zero component. Orthogonal force vectors can be three-dimensional with the third component being at right-angles to the other two.
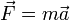
No comments:
Post a Comment